Curious about the average rating of the entire IMDB collection?

PS - That too, without ever needing to access the entire collection!

IMDB has more than a MILLION titles with ratings. Ever wondered what would the average rating for all 1M titles be?

I calculated it without scraping all 1M titles. Curious how?

IMDB has a staggering database of about 7M titles (movies, short movies, tv series, etc) - of them about 1M titles also have rating information

For eg, this movie(and a great one) has a rating of 7.9/10 (as voted by 170,392 voters)

What if I asked you "Can you figure out the average rating of IMDB, i.e. the average rating including all 1M titles?"

Can you? Of-course you can.

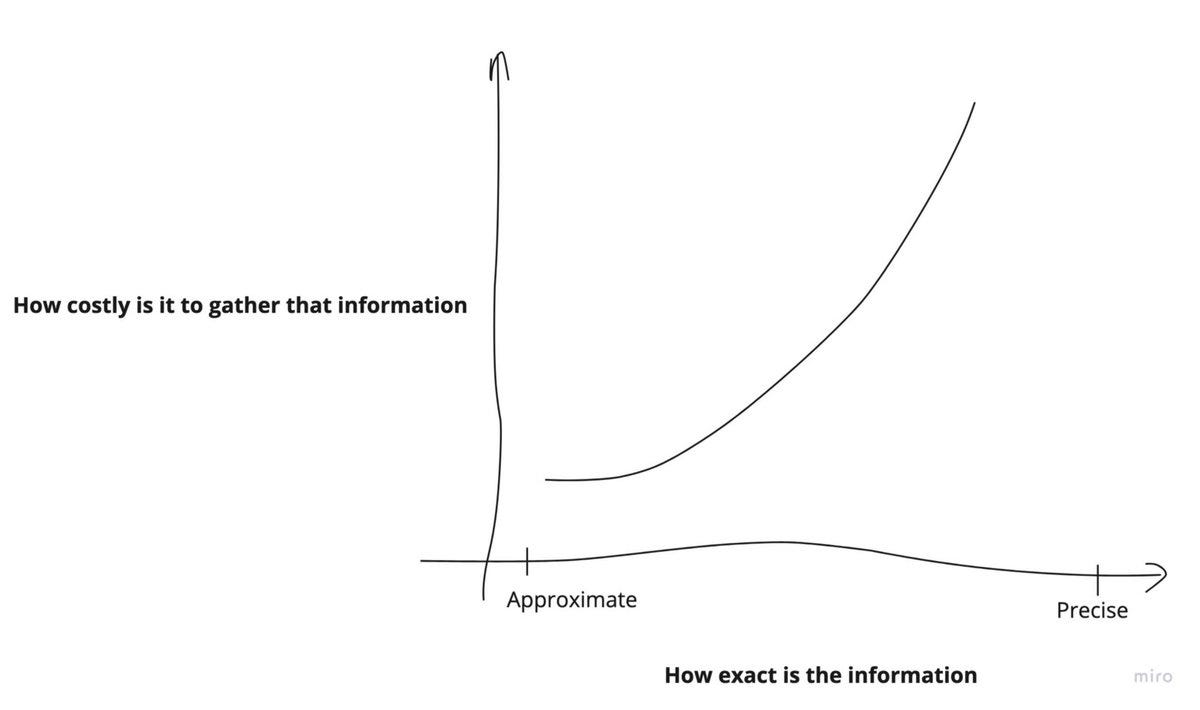
The question is, at what cost?

Is it worth your time/money/resources? Probably not

But what if we could "estimate" the population's average rating (when I say population, I mean the population of all 1M titles) without having to observe every single title? Now that would be something, right!

Now I know you could argue about the merit of an "estimate" v/s a "precise number", but remember - if you factor in the cost of getting precise information v/s the value you derive from cheap and good enough approximations, latter work really well

In-fact, that's how we operate in the real world; we approximate information while tweaking the Signal/Noise ratio

Back to the estimation part.

The way our estimate would work is by coming up with a range… Something like "the population's average rating lies between <x>and <y>"

Next, we need samples. Samples of what? Samples from the population of 1M titles

A word of caution - these samples have to be random.

What I means is, we shouldn't choose titles from our favourite genre or avoid movies that star Nicolas Cage. That sample would reflects our bias, and we don't want that

Now to make this more enjoyable for you, I have already taken few samples at random from the entire population of 1M titles - This data is public btw (https://imdb.com/interfaces/)

All you have to do is choose any no from the GIF below  -- the number you see will be the no of samples I will take --> then do some weird magic and report back my estimate

Want to test? Say you choose a 5.

With 5 random samples, I estimate the population average(i.e the average rating across all titles) to be b/w 4.81 and 7.51

Another one? Say you choose 500.

With 500 random samples, I estimate the population average to be b/w 6.79 and 7.03

You might ask me about how confident I am about each one of my estimates -  I'd be wrong 5 out of 100 times

In other words, the weird magic that I did to estimate the population's average rating would work 95 out of 100 times (not that bad)

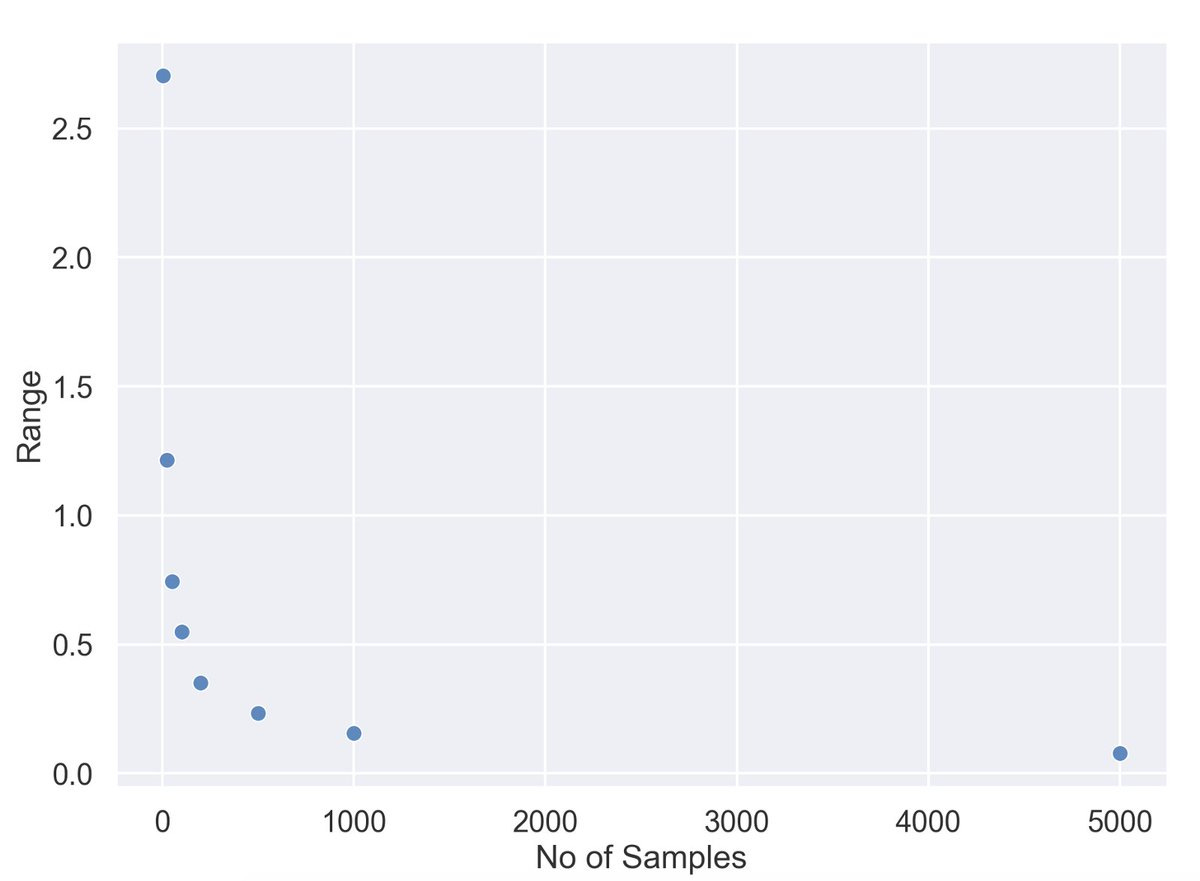
Now I know you are an astute reader; did you notice any trend above - b/w the width of our range and the no of samples we took

With 5 samples, we were looking for our population average b/w 4.81 and 7.51, that's a whooping spread of 2.7 units. This kind of approximation is no good clearly

But with 500 samples, we were able to shrink that range to a mere 0.24 units!

This means the more samples you can take, the shorter the range of your estimate gets.

In other words, the more samples you take, the closer you get to the true average

Notice with 5000 samples, you have the narrowest range b/w 6.83 and 6.91

Ready for an amazing revelation?

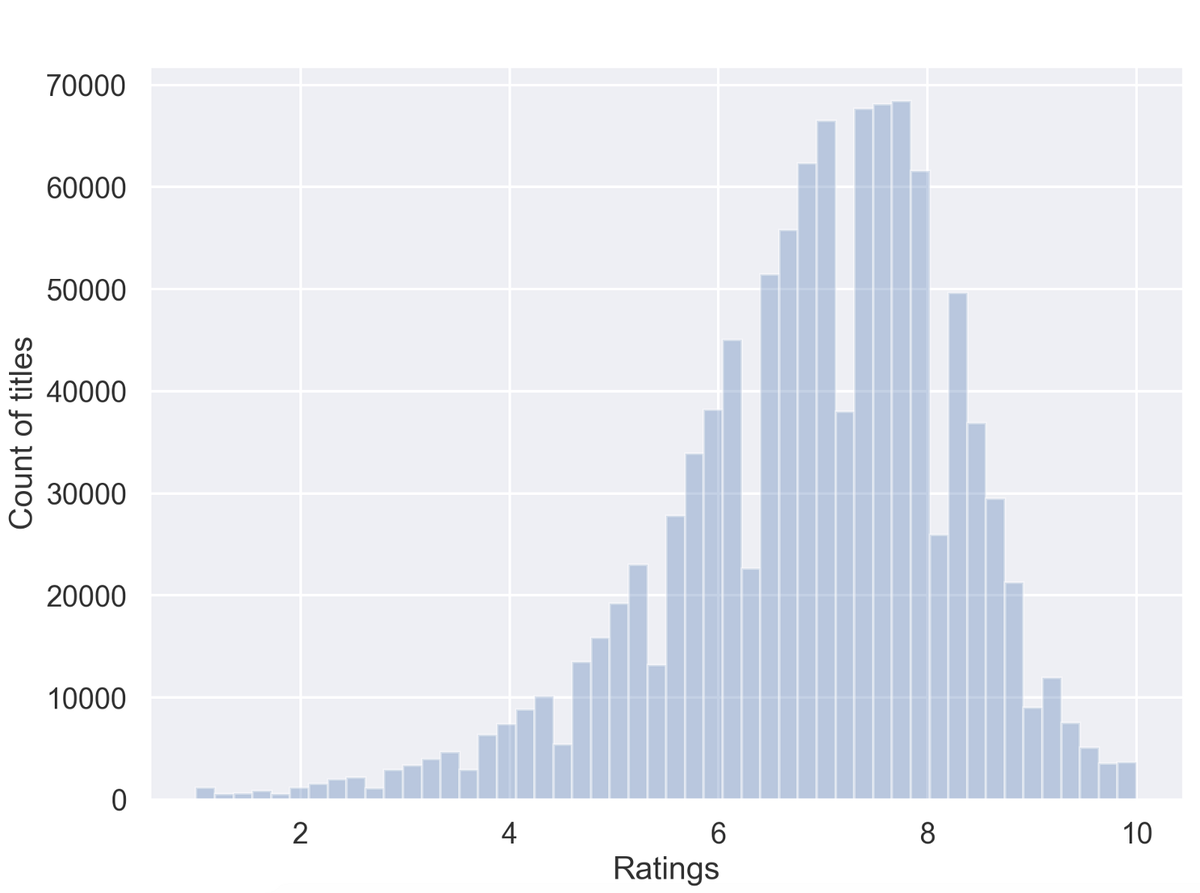
The true IMDB average rating of all 1M titles is …… 6.88 🤯🤯🤯

On that note, this is the true distribution of all 1M titles on IMDB with a nice Left skew

Isn't that amazing?

With as few as 100 samples, we were able to estimate that average rating of 1M titles b/w 6.5 and 7.04 WITH JUST 100 SAMPLES!

The weird magic that I talked about, brainy folks call it the Central Limit Theorem(CLT) - It allows me to estimate information (with some level of confidence) about a population, with as few as 50/100 samples - Taken from that same population and at random

The next time you are wondering what your users think about a new flow, a new feature or the 50 shades of Blue, remember - You don't need 1000s of samples to wait for precise information, you can always approximate

I took the liberty to avoid a lot of details to lead the reader straight to the idea  that -- We need "less data" than we think, and we have "more data" than we think

Hope you enjoyed this gentle introduction to Central Limit Theorem and a practical application of the same,

Until next time, happy approximations!